My team was dealing with a large flow, where user can transition from multiple states or sometimes skip certain states. We didn’t have a centralized controller, every screen just had logic on where it should go next.
This made it difficult for us to see all our logic at once. We asked around and was told state machines are a good fit for our situation.
State machines are void of any UX. You just pass an event to it. Based on the event and the current state, you update to a new state along with an optional command to act upon.

A watered down example of a State machine is:

Current state         +     Event             ->   Command    ->    New state
-----------------------------------------------------------------------------------
.houseIsClean         + .momEnteredHome       -> nil          ->   (no state change)
.houseWasAMess        + .momEnteredHome       -> .cleanHouse  ->   .cleaningHouse
.cleaningHouse        + .houseGotCleaned      -> nil          ->   .houseIsClean

.houseIsClean         + .guestsWillCome       -> .makeFood    ->   .makingFood
.makingFood           + .foodPrepared         -> nil          ->   .waitForAllGuests
.waitForAllGuests     + .allGuestsArrived     -> .serveDinner ->   .eating

Now let’s see how that can be deemed similar to graphs…

Interview Question

You are climbing stairs. It takes n steps to reach the top.

Each time you can either climb 1 or 2 steps.

In how many distinct ways can you climb to the top?

Example if there are 3 steps to the top, then you can do:

- 0 --jump1--> 1 --jump1--> 2 --jump1--> 3 
- 0 --jump1--> 1 --jump2--> 3
- 0 --jump2--> 2 --jump1--> 3

Let’s draw a graph for counting how many ways we can get to 3: “tree”

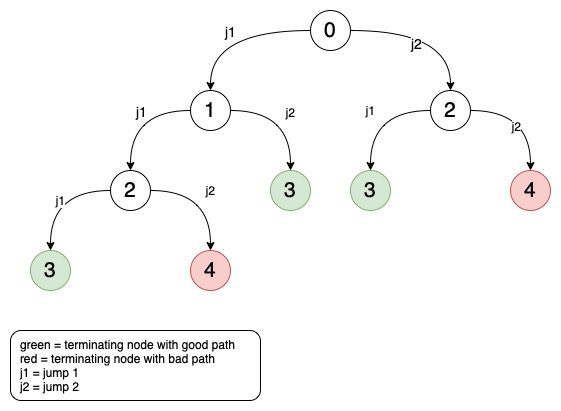
How Graphing is similar to state machines:

Not 100% similar, but to a certain point: when we apply the same concept:

apply command + state -> event - - - > calculate new command
------------------------------------------------------------
No command + from 0 -> from 0 - - - > jump 1 & jump 2
    jump 1 + from 0 -> arrive at 1 - - - > jump 1 & jump 2
        jump 1 + from 1 -> arrive at 2 - - - > jump 1 & jump 2
            jump 1 + from 2 -> arrive at 3 - - - > terminate
            jump 2 + from 2 -> arrive at 4 - - - > terminate
        jump 2 + from 1 -> arrive at 3 - - - > terminate
    jump 2 + from 0 -> arrive at 2 - - - > jump 1 & jump 2
        jump 1 + from 2 -> arrive at 3 - - - > terminate
        jump 2 + from 2 -> arrive at 4 - - - > terminate

It’s important to note that:

  • The only possible commands are ‘jump 1’ and ‘jump 2’. (If we were allowed to jump 3 steps, then ‘jump 3’ would have been another command as well)
  • However the current state can be a different number each time.
  • From each state we bifurcate to apply two new commands.
  • Because we bifurcate, we have to add the result (number of paths that lead to step n from node m) of the two branches.
  • A code-path terminates when it reaches n or above.
    • If we reach n exactly then we return 1.
    • If go over n, then we return 0.
  • In state machines, once you reach the terminating event, then your state machine is finished. However since we’ve bifurcated multiple times, the exploring will only terminate when all branches terminate.

💡Summary:

  • An Edge in a graph is like an command in a state machine.
  • The current node in a graph is like the states in a state machine.
  • The next node in a graph is like the after result of handling a command in a state machine.
  • The end of a path is like reaching the end of a state machine.
  • A leaf branch of a base case is like terminating a state machine. Meaning state machine finishes i.e. the branch can’t recurse any more. In the tree example, base case is either if:
    • Target has been reached. (You reached the desired stair)
    • You’ve passed beyond your target. (You jumped pass the desired stair)

Code

func howManyWays(num: Int) -> Int {
    return helper(origin: 0, target: n)
}

func helper(origin: Int, target: Int) -> Int { 
    if origin == target {
        return 1
    } else if origin > target {
        return 0
    } else {
        return helper(origin: origin + 1,target: target) + helper(origin: origin + 2, target: target)
    }
}

print(howManyWays(num: 4))

Code using memoization/caching:

var cache: [Int: Int] = [:]
func howManyWays(num: Int) -> Int {
    return helper(origin: 0, target: num)
}

func helper(origin: Int, target: Int) -> Int {
    if let val = cache[origin] {
        return val
    }
    var ans: Int
    defer {
        cache[origin] = ans
    }
    
    if origin == target {
        ans = 1
        return ans
    } else if origin > target {
        ans = 0
        return ans
    } else {
        ans = helper(origin: origin + 1, target: target) + helper(origin: origin + 2, target: target)
        return ans
    }
}

💡 Summary - Appendix

  • If we’ve already handled a certain event + state combination, then we just store the output command in memory.
  • By doing this, we don’t need to re-calculate the command every time.

Difference between State Machine and Trees/Graphs

Does it matter how you got to a start node or state? Or all that matters is that you’re at a specific Node (event)?

A state machine usually doesn’t care how you arrived at a certain event. All it cares about is 1. event 2. state. Based on those two, it can come up with a command. However trees and graphs, often require to know exactly the previous nodes you traversed through to arrive at a certain point.

If you had a single path/branch through out your tree i.e. if it look liked a single line, then it would match with a state machine. However if you have multiple branches, which 99% of the time you do, then you must always:

  1. Keep an array to know how you arrived at a current node. Example you could arrive at node F from a path of [A, B] or [A, D, C]
  2. Update the path that was passed down to i.e. change it to [A, B, F], or [A, D, C, F]
  3. Pass the new path down to the next node.

Note: In the ‘How many ways you can climb’ example, we didn’t have a need to know what our current path is, but for other questions example Generate Parentheses you need to pass certain ‘path-specific’ variables down the path.

Tree vs a single branch

A tree is made up of multiple branches. States (or values of interest i.e. the answer/returned value) can be associated with:

  • The entire tree

    • The state is associated with the entire tree. You don’t need to pass it down your branch. You can just retrieve it from a property a class. Example: the can sum problem. It doesn’t matter if your sum of 7 was made through 5,2 or 2,2,2,1 or 4,3 or 7. All that matter is that you got there.

  • A single branch/path

    • The state is associated with the current path. You need to pass and update that value down your branch. Example: the generate parenthesis problem. You have to pass down how many parenthesis you’ve opened or closed so far.

Another Dynamic Programming Example:

  • Assuming you can travel in only the right and down direction of a grid: count the number of possible ways to reach from one corner of a 3 x 3 grid to another.
    • Our commands are only
      • move right
      • move down
    • Our events are:
      • arrived at grid (1,0)
      • arrived at grid (0,1)
      • arrived at grid (1,1)
      • …
      • arrived at grid (3,3)
    • Our terminating state is:
      • arrived at (4,0)…(4,3) or (0,4)…(3,4). Because anything passed the 3rd item in the grid — either vertically or horizontally is a terminating state or out of bounds…
    • State transitions that we don’t need to re-calculate over and over are:
      • storing the number of ways to reach to (3,3) from (3,2)
      • storing the number of ways to reach to (3,3) from (2,3)
      • storing the number of ways to reach to (3,3) from (2,2)
      • …
      • storing the number of ways to reach to (3,3) from (0,0)

Note:

Your graphs shouldn’t be cyclic otherwise you won’t be terminating/ending your graph or state machine. For this reason, State Machines are usually named ‘Finite State machines’.