Attention: This post was updated to include the alternate solution that uses binary search. It reduces the Time Complexity from O(n * n) to O(n * log n).

Before we present the question. Let’s figure out what a subsequence is:

What’s a subsequence?

Any selection of items from the original array. The selection must respect the order. Meaning for [1,2,3,4,5] only two of the four below are subsequences:

[1,2,3,4,5] ✅
[1,4,3,2,5] ❌ order not respected
[1,2,5] ✅
[5,1] ❌ order not respected

What’s the difference between a subsequence and a subarray?

Subarray, is just like subsequence, that is order must be respected. Additionally the sub-array has to be made of continuous elements.

[1,2,3,4,5] ✅
[1,2,3,5] ❌ gap 
[1,2,3] ✅
[2,4] ❌ gap

What’s a longest increasing subsequence?

This is also known as LIS.
For [0, 3, 1, 7, 5, 2, 8] the longest increasing subsequence is: [0,1,7,8].
For [2,2,2,2]. LIS is: [2].
For [3]. LIS is: [3]

In this post, we’re only going to calculate the length of the LIS. We won’t construct the actual subsequence itself. To learn how to construct the path, see here

Explanation

So this problem can be broken into subproblems i.e.

  • The LIS of index 6, depends on the LIS of all indices between 0-5.
  • The LIS of index 5, depends on the LIS of all indices between 0-4.
  • …
  • The LIS of index 1, depends on the LIS of index 0
  • The LIS of index 0, is 1. Because every element has a subsequence of 1.

Whenever we can turn our problem into subproblems, then Dynamic programming is a good candidate for finding a solution.
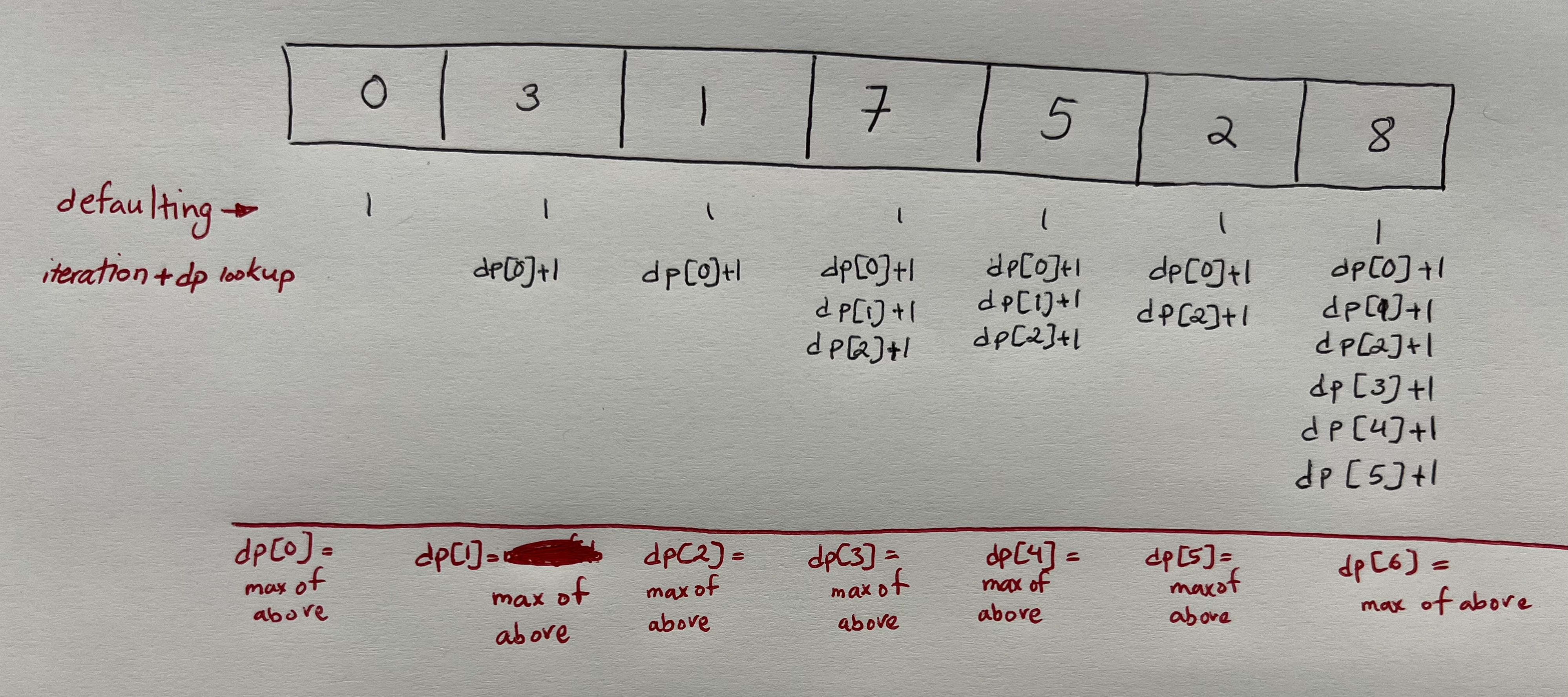
To do this, let’s create an array named dp to represent the the answer to the subproblem for a given index.

let arr = [0, 3, 1, 7, 5, 2, 8] We’ll create an array with the same length of our original array. Default all the values to 1. Example: var dp: [Int] = Array(repeating: 1, count: arr.count).
Let’s just assume we want to calculate the LIS all the way to index 4. And we’ve already updated the value for all previous indexes. How do you think we need to update dp[4]:

    [0, 3, 1, 7, 5, 2, 8]
                  ↑
                dp[4]

Which of the following would it be?

  1. The value for dp[4] will be max(dp[0] + 1, dp[1] + 1, dp[2] + 1, dp[3] + 1)
  2. The value for dp[4] will be max(dp[0] + 1, dp[1] + 1, dp[2] + 1)

The correct answer is the second line.
First line is incorrect because 7 is bigger than 5. dp[3] + 1 shouldn’t be considered.
This means that assuming there is at least one item in the array, the default value should then be 1.

In short:

  • For every index, we use compare its value with its previous indices
    • If current index is bigger, then we increase the LIS length between the two indices.
    • At any given index we perform a max between all nodes that were able to increase the subsequence to that point.
  • We do this till the end of the array.
  • Then do a max against our dp array.

Pro tip

Use a paper and go through this example again by yourself. Just compare any two indexes, add to the previous, do a max. I was then able to reason with it a lot lot easier on paper. Here’s what I wrote:

“LIS steps”
Longest Increasing Subsequence Length

Code

func lengthOfLIS(_ nums: [Int]) -> Int {
    var dp: [Int] = Array(repeating: 1, count: nums.count)
    
    for i in 0...nums.count - 1 {
        for j in 0..<i {
            if nums[j] < nums[i] {
                dp[i] = max(dp[i], dp[j] + 1)
            }
        }
    }
    
    return dp.max()!
}

Time Complexity

  • for-loop: O(n)
    • for-loop from beginning till current end index: O(n)

Total = O (n * n)

Space Compleixty

The dp array: O(n)

Important Notes:

Assuming your nodes are as such i.e. just a degenerate tree:

a -> b -> c -> d

  • A lot of times when you’re going from one node to the other, all you care about is going from node c, to node d. However in this question, it’s about an operation that goes from all previous nodes to this node. i.e. we need to calculate: a -> d, b -> d, c -> d and then do a comparison between them all. This is what makes this question unique. Because in the coin change example, all we needed to calculate things was from previous to next.

  • Most of the time when you want to memoize things you use a dictionary of type [Int: Int]. We could certainly do that here too. Here in this example, I used an array, because the video I saw was using an Array :). It intiially put me off, but I get it now.
    Like if all you need to do is add and access certain indexes and not search or remove items, then array and dictinary aren’t different so much.

  • Additionally in in this question, going from left to right or right to left don’t make a difference in terms of our answer.

    • If we start from the beginning, then each index will get added to all answers of its previous indicides — if it’s bigger than the value being compared to.
    • If we start from the end, then new each index will still get added to all answers of its next indicies — if it’s smaller than the value being compared to..

It really doens’t matter which way we select.

  • Any time you hear order, increasing, sorted, decreasing, then perhaps binary search is a helpful way of doing things. This isn’t always true, but in this case it is.
  • Think of binary search as an optimization mechanism. Not as a solution finder i.e. try to try to solve it first without a binary search. Then improve your solution using binary search.

Simply put create a list, append or replace items.

  • Append items that are bigger than the current biggest -> Help increase the length of the list.
  • Replace items that are smaller than the current biggest -> Helps reduce the bar for adding smaller items to the list.
  • Note: Such a list like this won’t always end up being a real LIS, only that it will have correct length of the LIS.

It’s hard to explain it with words. I’ll try to explain it with just two examples, but also see this video as well. Maybe even before this.

Example1:

[0, 15, 1, 7, 5, 4, 8, 3]

list = []
[] + 0 -> [0] we're expanding the list. 
[0] + 15 -> [0, 15] we're expanding the list.
[0, 15] + 1 -> [0, 1] we've replaced our biggest value with 1. This makes the list acceptable for smaller numbers as its next addition i.e. if 15 was kept then no other number from the list could have been added. 

[0, 1] + 7 -> [0, 1, 7] we're expanding the list. 
[0, 1, 7] + 5 -> [0, 1, 5] we've replaced our biggest value with 5. This makes the list acceptable for smaller numbers as its next addition i.e. if 7 was kept then we would have not been able to add 2.
[0, 1, 5] + 4 -> [0, 1, 4] we've replaced our biggest value with 4. This makes the list acceptable for smaller numbers as its next addition.

[0, 1, 4] + 8 -> [0, 1, 4, 8] we're expanding the list. 
[0, 1, 4, 8] + 3 -> [0, 1, 3, 8] we've replaced the first/smallest item that's bigger than 3. This makes the list acceptable for smaller numbers as its next addition — while maintaining its order. We find the index to replace by doing a 'search to find the first index that has a value that's smaller than the new item (3) but also that the value at its next index (4) is greater than the new item.

Note: While the replacement doesn’t change the length, it improves the quality of the list by making it more likely to accept future additions. Future additions which will ultimately shrink down the last item. Which then means more smaller items can get appended. This is important because the search algorithm that we are using to find the insertion point for the new element depends on the list being sorted. If you’re still confused about this step, then see Example 2. It better demonstrates why we’re doing this.

Example2:

[0, 5, 15, 2, 3, 4]


list = []
[] + 0 -> [0]
[0] + 5 -> [0, 5]
[0, 5] + 15 -> [0, 5, 15]

[0, 5, 15] + 2 -> [0, 2, 15] <- Made list more acceptable for smaller numbers to be appended. If we can get rid of 15, then we're in a much stronger position to append numbers to the list. 
[0, 2, 15] + 3 -> [0, 2, 3] <- We did it! Got rid of 15. We have a good chance of appending a new value. 
[0, 2, 3] + 4 -> [0, 2, 3, 4] <- Appended new value!

Code

class Solution {
    func lengthOfLIS(_ nums: [Int]) -> Int {
        var lis: [Int] = []
        
        guard nums.isEmpty == false else {
            return 0
        }
        
        for num in nums {
            // If it's bigger than biggest then append it
            if num > lis.last ?? Int.min {
                lis.append(num)
            // if it's smaller than smallest then replace the smallest. 
            } else if num < lis.first ?? Int.max {
                lis[0] = num
            } else {
                // find a suitale place to replace it  
                searchAndReplace(num, in: &lis, startIndex: 0, endIndex: lis.count - 1)
            }
        }
        return lis.count
    }
    
    /// Finds the correct replacing index from within a specific range. Then replaces it. 
    /// If bigger than middle && smaller than next element after middle index then replace the element after the middle index. 
    /// Example: If list is `1,3,5` and we're trying to add `4`, then since 4 is greater than 3 but less than 5, we'll replace 5, with 4. 
    /// tldr the binary search isn't to find an exact item. It's more of finding the first/smallest item that's bigger than our `num` field. 
    /// - Parameters:
    ///   - num: new number to get added
    ///   - arr: current list of items
    ///   - startIndex: start index to search into
    ///   - endIIndex: end index to search into
    func searchAndReplace(_ num: Int, in arr: inout [Int], startIndex: Int, endIndex: Int) {
            let middle = (endIndex + startIndex) / 2
            
            if num == arr[middle] {
                // do nothing
            } else if num > arr[middle] && num <= arr[middle + 1] {
                arr[middle + 1] = num
            } else if num > arr[middle] {
                searchAndReplace(num, in: &arr, startIndex: middle + 1, endIndex: endIndex)
            } else {
                searchAndReplace(num, in: &arr, startIndex: startIndex, endIndex: middle - 1)
            }
        }
}

I must admit, it’s hard to come up with the idea for such a solution. To come up with the idea for this question you have to iteratively improve it. Something like:

  • I see “increasing”. Perhaps I can create something sorted and keep it sorted.

  • Focus on the number of items and not actual subsequence.

  • Once I found a solution through linear search, then maybe I can build on top of it and go with a binary search instead to optimize.

  • What makes it counter-intuitive is to figure out how a bigger subsequence is replaced with a smaller subsequnce. Example from [80, 81, 82, 1, 2, 3, 4], how to replace the current [80,81,82] with [1,2,3,4] which is really the heart of it. The idea is to zip-merge together all sequences in an increasing order knowing that any number that’s bigger than the current biggest will enlarge the sequence for the current longest.

Time Complexity

for-loop: O(n)

  • search and find: O(log n) – Assuming you’re using ‘binary search’

Total: O(n * log n)

Memory Complexity

O(n)

Other Questions that use LIS:

See my post on How many envelopes can you fit into another a.k.a the Russian Doll Envelope question.

Acknowledgements

Shout out to Take U forward for their YouTube post. I wasn’t able to get a good grasp on the binary search approach without it.